14635次 ] 文档 代码 工具 在VC++实现数据加密
作者：惠州市东晓电子有限公司　龚辉斌

下载本文示例源代码

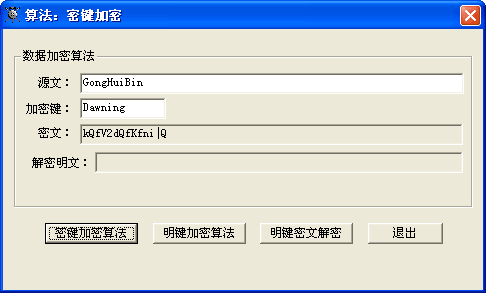
为了保证数据的安全性与完整性，常常要对数据进行加密，在数据传输过程进行数据加密可以防止中途非法截获。我们通常称原始数据叫做源文，用约定的加密算法进行加密处理。加密算法的输入是源文与加密键，而输出的则是密文。加密算法可以分为两种，一种是密键加密算法，一种是明键加密法。



一、密键加密法：
　　加密算法可以公开，但加密键一定要保密。密文对不知道加密键的人来说，是不容易解密的。如下述算法：
A．把源文分成等长的块，每块的长度和加密键的长度相等，对长度不够的块用空格补充；
B．用自己定义的整数代替源文的数据；
C．对加密键也进行数据替换操作；
D．对源文的整数码与加密键相应字符的整数码进行相加，然后对某一整数进行取模操作；
E．将整数码再用相应的字符进行替换，这样就得到了密文。
实现代码如下：

CString CEncryptDlg::Encrypt_Key(CString Source,CString Key)

{

	int iSourceLen,iKeyLen;

	int iCount;

	div_t div_Result;

	char strTarget[255];

	char pKey[255],pSource[255],pMid[255];

	CString strTmp;

	int i,j,n;

	BYTE PWD_key[255];



	j=0;

	for (i=32;i<=126;i++)

	{

		PWD_key[i]=j;

		j++;

	}//取ASCII值在32~126之间的可视字符



	iSourceLen=Source.GetLength();

	iKeyLen=Key.GetLength();

	div_Result=div(iSourceLen,iKeyLen);

	if (div_Result.rem)

		iCount=div_Result.quot+1;

	else

		iCount=div_Result.quot;

	wsprintf(pKey,"%s",m_Key);



	n=0;

	for (i=1;i<=iCount;i++)

	{

		strTmp=Source.Mid((i-1)*iKeyLen,iKeyLen);

		if (strTmp.GetLength()<iKeyLen)

		{

			for (j=1;j<=iKeyLen-strTmp.GetLength();j++)

				strTmp+=" ";

		}

		wsprintf(pSource,"%s",strTmp);



		for (j=1;j<=iKeyLen;j++)

		{

			int k1;

			int k2;

			k1=PWD_key[pKey[j-1]];

			k2=PWD_key[pSource[j-1]];

			int k=k1+k2;

			div_Result=div(k,ENCRYPT_KEY);

			k=div_Result.rem;

			pMid[j-1]=k;

			strTarget[n++]=k;

		}//对源文进行替换加密处理



	}

	for (j=0;j<n;j++) 

	{

		strTarget[j]+=32;

		if (strTarget[j]==32) strTarget[j]=''*'';  //用“*”替代密文中的空格

	}

	strTarget[n]=''\0'';



	CString strResult;

	strResult.Format("%s",strTarget);

	return(strResult);

}

　注：对D步的数据处理，每人也可以根据自己的具体情况用别的计算方法替换。

二、明键加密算法
　　明键加密算法可以随意使用加密算法与加密键，但是解密键是保密的。所在，它同时需要两个键，一个用于加密，一个用于解密。而解密键不能从加密键推出的。从而，每个人都可以对源文进行加密操作，但是在没有授权进行解密时，他是不能完成解密工作的，因为他不知道解密键。具体算法如下所述：
A．任意选择两个质数p与q，它们取值最好在100位左右。同时计算r=p*q；
B．任意选择一个整数e，e是与(p-1)*(q-1)互为质数的，e就是算法中的加密键；
C．求解方程式：(d*e) mod ((p-1)*(q-1))=1，d即是加密算法中的解密键；
D．对源文p进行加密即可得到密文，计算公式为c=pe mod r；c即为密文；
E．对密文c进行解密即可得到源文，计算公式为p=cd mod r；p即为源文；

加密算法实现如下：

CString CEncryptDlg::Encrypt_KnownKey(CString Source)

{

	int r=ENCRYPT_P*ENCRYPT_Q;

	int e=101;  

	//设置加密键，一般比P与Q大的质数就可以选作加密键

	int k=(ENCRYPT_P-1)*(ENCRYPT_Q-1);

	int d=5;

	//求得解密键，即满足公式：(d*11) mod k=1



	char pSource[255];

	char pTarget[255];

	int iLen;

	int i;

	DWORD dw1;



	wsprintf(pSource,"%s",m_Source);

	iLen=m_Source.GetLength();

	for (i=0;i<iLen;i++)

	{

		div_t div_Result;

		dw1=Exp(pSource[i],e,r);

		div_Result=div(dw1,r);

		pTarget[i]=div_Result.rem;

		//获取密文

	}

	pTarget[iLen]=''\0'';



	CString strTarget;

	strTarget.Format("%s",pTarget);

	return(strTarget);

}

解密算法如下：

CString CEncryptDlg::Decode_KnownKey(CString Source)

{

	int r=ENCRYPT_P*ENCRYPT_Q;

	int e=101;  

	//设置加密键，一般比P与Q大的质数就可以选作加密键

	int k=(ENCRYPT_P-1)*(ENCRYPT_Q-1);//k=168

	int d=5;

	//求得解密键，即满足公式：(d*29) mod k=1



	int iLen=m_Source.GetLength();

	char pSource[255],pTarget[255];

	wsprintf(pSource,"%s",m_Source);

	for (int i=0;i<iLen;i++) 

	{

		DWORD dw1;

		dw1=Exp(pSource[i],d,r);

		div_t div_Result;

		div_Result=div(dw1,r);

		pTarget[i]=div_Result.rem;

	}

	pTarget[iLen]=''\0'';



	CString strTarget;

	strTarget.Format("%s",pTarget);

	return(strTarget);

}

本文仅列出了最基本的算法实现，只是为了抛砖引玉。
程序在Windows XP + VC++ 6.0下调试通过。
作者信箱：devvy@{域名已经过期}。