西安空军工程大学工程学院,西安 710038
胡金山,朱青云,余治国

下载源代码


我们在学习有限元课程时做的另一个作业，用 C/C++ 编程求解了一个简单的有限元问题，可以作为有限元学习的编程实例，以更好地理解有限元理论，并为进一步使用大型有限元软件打下基础。本文所涉及的有限元基本理论请参考章本照先生编著的《流体力学中的有限元方法》PP.156-165。

一、二维传热问题
如图一所示：


图一 二维传热问题

二、解题过程

• 1、对结构进行离散化，将待分析的结构物从几何上用线或面划分为有限个单元，按结构物的不同和分析要求，选取不同形式的单元，在单元的边界上设置节点，并书写编号。计算节点坐标
• 2、单元分析：设法导出单元的结点位移和结点力之间的关系，建立单元刚度矩阵。
  单元刚度矩阵的计算：
  对于方程
  
  
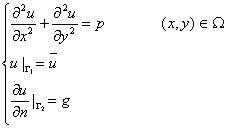
  采用 Galerkin弱解表达式
  
  （*）
  
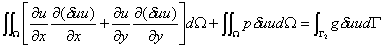  这里采用三节点的三角形单元，单元的基函数共有三个，选用插值多项式
  
  
  
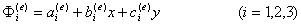
  分别代入单元三个节点的坐标可解得
  
  
  
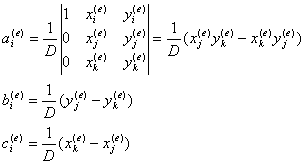
  其中
  
  
  
  
  
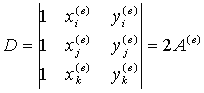
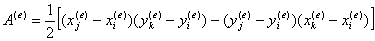
  e单元中的近似函数为
  
  （**）
  
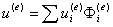  将式（*）中的积分区域取为e单元的区域 ，并将单元中的近似函数表达式（**）代入，并注意到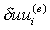的任意性，可得
  
  
  
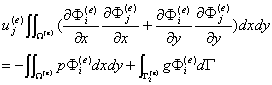
  记 （***）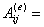
  
  （****）
  
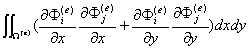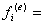
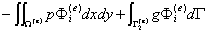  将单元基函数的具体表达式（*）代入（***）式中，可得
  
  
  
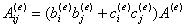
  通过等参变换（具体见文献1第201页），可得
  
  
  
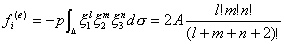
  这里指p为常数的情况，A为三角形单元的面积。
  
  
  
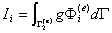
  这里g 均为0，所以此项不用计算。
  
  
• 3、整体分析（以求结点力为例） 整体分析就是将各个单元组成结构整体进行分析。整体分析的目的在于导出整个结构结点位移与结点力之间的关系，建立整个结构的刚度方程。 分析步骤：首先按着一定的集成规则，将各单元刚度矩阵集合成结构整体刚度矩阵，并将单元等效结点荷载集合成整体等效结点荷载列阵；然后引入结构的位移边界条件，求解整体平衡方程组，得出基本未知量――结点位移列阵。
• 4、用选定的算法语言编写出程序（C/C++），调试程序调用高斯消元法解方程的出结果。

附件程序Fem1.cpp计算了积分值，Fem2.cpp则采用了面积坐标下的插值函数，积分值取为三角形面积的三分之一。两者结果相同，但是后者更为通用，可以把程序用于其他形状的二维区域的有限元计算，Fem3.cpp计算了题2。

三．单元网格划分
四边形单元网格划分单元网格划分示意如图一：


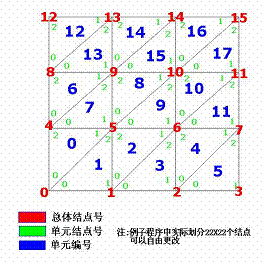
图一

计算结果结果数据可视化如图二、图三。它们是题1分别用Fem1.cpp程序和Fem2.cpp程序计算结果的Matlab数据可视化图，它们表现的数据基本一致，观察视点不同。图4是题2的解。


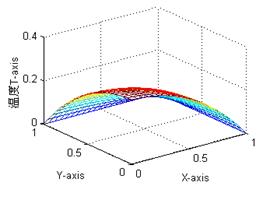
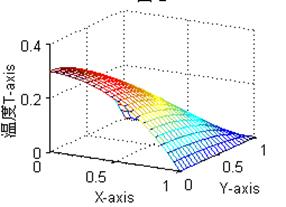
                图二                             图三



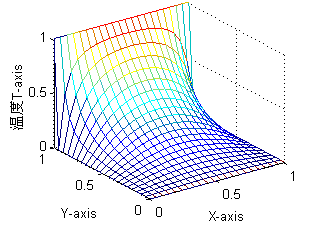
                图四

利用此程序的基本框架，我们还成功地解算了三角形、椭圆形区域的有限元问题。
最后感谢我们的老师----在数学和计算上具有深厚功力的王旭教授，感谢他对我们的悉心指导和热情鼓励！

参考文献：
1.章本照. 流体力学中的有限元方法[M]. 机械工业出版社, 1986