旋转的位棋盘
发布时间:2008-11-20
点击:
来源:本站原创
录入者:James Swafford
【编者的点评:这篇文章误导了我近半年,而事实证明 James Swafford 的 Galahad 并不算是成功的引擎,现在互联网上已经找不到它的资料了。我在这里提醒读者用怀疑的眼光来看本文(包括我的注解)。】
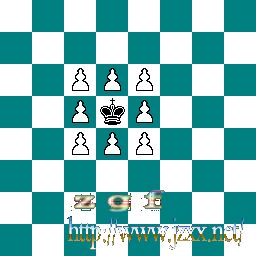
“位棋盘”可以记录的最有用的棋盘状况之一就是“棋盘上哪些格子受到某一特定棋子的攻击”。幸运的是,这样的计算耗时不多。对于那些活动能力不强的棋子,这可以说非常容易(请看上节“位棋盘”) 。原因是:当马,国王或兵在特定格子上时,无论周围情况怎样变化,所攻击的格子数目不变。你不用管那些格子上是否有棋子或者周围是否有特殊情况。
| 马在D5格可以攻击到的格子 |
国王在D5格可以攻击到的格子 |
黑棋的兵在D5格可以攻击到的格子 |
 |
 |
 |
- 但是对于车,象和皇后,事情就不那么简单了。例如,车攻击横线方向和竖线方向上的格子,直到在这两个方向遇到第一个有棋子的格子为止(包括这个有棋子的格子);如果没有遇到有棋子的格子,则到棋盘边界为止。也就是说,车所在横线和竖线上的棋子分布情况不同,受到这个车攻击的格子的数量也不一样。因为每条横线或竖线都有8个格子,每个格子又有2种状态(有棋子或者没有棋子),所以每条横线或竖线都会有28(256)种棋子分布状态。
-
- 用旋转的位棋盘计算受车攻击的格子
-
- 如何获得整个棋盘上受到某个车攻击的格子呢?最简单的方法是:先计算出一个位棋盘记录车所在横线上受其攻击的格子,在计算出另一个位棋盘记录车所在竖线上受其攻击的格子,最后用“逻辑或”把这两个位棋盘“结合”到一起。
- 整个操作的关键在于“预先计算”。对于64格中的每一格,都预先计算出当车在这一格时,不同情况下横线上受到攻击的格子(共256种情况)和不同情况下竖线上受到攻击的格子(也是256种)。当要寻找某一情况下受车攻击的格子时,用横线(或竖线)上的“棋子分布状态”作索引从预先计算出来的位棋盘数组中取得。
- 所以,第一步:预先计算出数组rank_attacks[64][256]和file_attacks[64][256]。
-
- /* 车或后横向移动的预先计算 */
- for (棋盘上的每一格)(0-63) {
- for (每行的棋子分布状态)(0-255) {
- 计算该状态下被占的格子
- 计算从这个格子朝左走的着法
- 计算从这个格子朝右走的着法
- rank_attacks[格子][横线状态] = attack_board;
- }
- }
- /* 车或后纵向移动的预先计算 */
- for (棋盘上的每一格)(0-63) {
- for (每条纵线的棋子分布状态)(0-255) {
- 计算该状态下被占的格子
- 计算从这个格子朝上走的着法
- 计算从这个格子朝下走的着法
- file_attacks[格子][纵线状态] = attack_board;
- }
- }
-
- 第二步:索引rank_attacks[64][256],数组的第一个索引号为车所在格的编号。第二个索引号为车所在行上的“棋子分布状态”。
- 请看下面这个例子:
| 车在E6格可以攻击到的格子 |
 |
- 第一个索引号是E6格的编号。在我的程序里,它的编号是20。第二个索引号是棋盘上第六行的棋子分布状态。
- 0 1 0 1 0 0 1 0
- 【编者注:在James Swafford的程序里,由于A8格编号为0,所以这串数据的顺序正好和棋盘相反,跟黑方看上去的顺序相同。】
- 要分离出上面这个数字,我们需要对位棋盘执行一个“位移(shift)”和一个“逻辑与”指令。在我的程序中,A8格的编号为0。如果车在第8行的任意格子上则不需要执行位移;若在第7行则要右移8位;在第6行要右移16位;以此类推。
| 需要右移的位数 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
| 16 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
| 24 |
24 |
24 |
24 |
24 |
24 |
24 |
24 |
| 32 |
32 |
32 |
32 |
32 |
32 |
32 |
32 |
| 40 |
40 |
40 |
40 |
40 |
40 |
40 |
40 |
| 48 |
48 |
48 |
48 |
48 |
48 |
48 |
48 |
| 56 |
56 |
56 |
56 |
56 |
56 |
56 |
56 | |
- 我们需要第6行的棋子分布情况(从第16位到第23位),就右移16位,现在它被右移到了最低的8位,我们把它与255(0xff)做逻辑与运算。所得到的东西即是我们需要作为rank_attacks的第二个索引号的数字。
-
- 第三步:索引数组file_attacks[64][256]。
- 如何计算出file_attacks位棋盘呢?还是通过索引数组。和上面一样,第一个索引号是车所在格的编号。第二个索引号是车所在列的棋子分布状态。
- 1
- 0
- 0
- 0
- 0
- 1
- 0
- 1【编者注:同样道理,这是黑方看上去的位置。】
- 要分离出这个索引号比分离rank_attacks的要复杂一些。仅执行“位移”和“与”指令是无法做到的。首先,我们要把棋盘右转90度【编者注:即顺时针转90度。】。因此现在它看上去应该是这个样子:
| 右转90度后的棋盘 |
 |
- 这个旋转后的棋盘是怎么得到的?你可以在开始做下一层搜索的时候构建这个棋盘,或者简单地在“走”下一步棋或“恢复”上一步棋的时候逐步更新它。下面的方法演示了如何在开始做下一层搜索时构建它。(代码并不那么优雅,但较易理解……)
-
- int r90R_map[64] = {
- H8, H7, H6, H5, H4, H3, H2, H1,
- G8, G7, G6, G5, G4, G3, G2, G1,
- F8, F7, F6, F5, F4, F3, F2, F1,
- E8, E7, E6, E5, E4, E3, E2, E1,
- D8, D7, D6, D5, D4, D3, D2, D1,
- C8, C7, C6, C5, C4, C3, C2, C1,
- B8, B7, B6, B5, B4, B3, B2, B1,
- A8, A7, A6, A5, A4, A3, A2, A1
- };
- BitBoard Rotated90R = 0;
- for (棋盘上的每一格)(0-63) {
- if (格子被占)
- Rotated90R |= mask[r90R_map[square]];
- }
-
- 这样,原来在A8格上的棋子被“映射”到H8格上,原来在H8格上的棋子则被“映射”到H1格上……
- 现在,我们可以对这个旋转后的位棋盘执行“位移”和“与”操作了。
-
- 第四步:获得rook_attacks位棋盘。
- 得到rank_attacks和file_attacks位棋盘后,你只要简单的对这两个位棋盘执行“与”运算就获得了记录了所有受到那个车攻击的格子的位棋盘了。
-
- rook_attack = rank_attack | file_attack;
-
- 用旋转的位棋盘计算受象攻击的格子
-
- 计算受象攻击的格子的方法与车类似。对应于车的把横线与竖线做“或”运算,这里我们对象所在的两条斜线做“或”运算。我们把第一条斜线(就是执白时,从左上到右下这条斜线)叫做diag_A8H1;另一条斜线叫做diag_H8A1。相对车这里还多了一步,原因是每条斜线的长度不同。先预先计算出数组diag_A8H1_attacks[64][256]和diag_H8A1_attacks[64][256]。A8格编号为0,H8格为7,A1格为56,H1格为63。
-
- int length_A8H1_diag[64] = {
- 8, 7, 6, 5, 4, 3, 2, 1,
- 7, 8, 7, 6, 5, 4, 3, 2,
- 6, 7, 8, 7, 6, 5, 4, 3,
- 5, 6, 7, 8, 7, 6, 5, 4,
- 4, 5, 6, 7, 8, 7, 6, 5,
- 3, 4, 5, 6, 7, 8, 7, 6,
- 2, 3, 4, 5, 6, 7, 8, 7,
- 1, 2, 3, 4, 5, 6, 7, 8
- };
- int length_H8A1_diag[64] = {
- 1, 2, 3, 4, 5, 6, 7, 8,
- 2, 3, 4, 5, 6, 7, 8, 7,
- 3, 4, 5, 6, 7, 8, 7, 6,
- 4, 5, 6, 7, 8, 7, 6, 5,
- 5, 6, 7, 8, 7, 6, 5, 4,
- 6, 7, 8, 7, 6, 5, 4, 3,
- 7, 8, 7, 6, 5, 4, 3, 2,
- 8, 7, 6, 5, 4, 3, 2, 1
- };
- /* 象或后在A8-H1方向移动的预先计算 */
- for (棋盘上的每一格)(0-63) {
- /* 状态数会随对角线长度而变化 */
- for (每条对角线的棋子分布状态)(0-(2^对角线长-1)) {
- 计算该状态下被占的格子(注意某些状态不要把8个格子都考虑进去)
- 计算从这个格子朝左上方走的着法
- 计算从这个格子朝右下方走的着法
- diag_A8H1_attacks[格子][状态] = attack_board;
- }
- }
- /* 象或后在H8-A1方向移动的预先计算 */
- for (棋盘上的每一格)(0-63) {
- /* 状态数会随对角线长度而变化 */
- for (每条对角线的棋子分布状态)(0-(2^diag length)-1) {
- 计算该状态下被占的格子(注意某些状态不要把8个格子都考虑进去)
- 计算从这个格子朝右上方走的着法
- 计算从这个格子朝左下方走的着法
- diag_H8A1_attacks[square][diag state] = attack_board;
- }
- }
-
- 索引 diag_A8H1_attacks[64][256] 数组。
- 不说你也应该知道,第一个索引号是象所在格的编号。第二个索引号是它所在A8->H1方向斜线上的棋子分布情况。没错,接下去又要旋转位棋盘,位移,最后用“逻辑与”分离出我们需要的东东。为了对齐 A8->H1 斜线上的格子,我们要把棋盘左转45度。(现在我建议你去拿罐可乐,外加一些提神的药物……)
-
- int r45L_map[64] = {
- 28, 21, 15, 10, 6, 3, 1, 0,
- 36, 29, 22, 16, 11, 7, 4, 2,
- 43, 37, 30, 23, 17, 12, 8, 5,
- 49, 44, 38, 31, 24, 18, 13, 9,
- 54, 50, 45, 39, 32, 25, 19, 14,
- 58, 55, 51, 46, 40, 33, 26, 20,
- 61, 59, 56, 52, 47, 41, 34, 27,
- 63, 62, 60, 57, 53, 48, 42, 35
- };
-
- 注意每个格子的映射次序,是从右上往左下的。这样映射后的位棋盘就会沿着A8-H1斜线对齐了(所有的斜线都是沿着这个方向走的)。
-
- BitBoard Rotated45L = 0;
- for (棋盘上的每一格)(0-63) {
- if square is not empty
- otated45L |= mask[r45L_map[square]];
- }
-
- 现在“右移”这个棋盘,但是移动几位呢?
|
需要右移的位数 |
| 28 |
21 |
15 |
10 |
6 |
3 |
1 |
0 |
| 36 |
28 |
21 |
15 |
10 |
6 |
3 |
1 |
| 43 |
36 |
28 |
21 |
15 |
10 |
6 |
3 |
| 49 |
43 |
36 |
28 |
21 |
15 |
10 |
6 |
| 54 |
49 |
43 |
36 |
28 |
21 |
15 |
10 |
| 58 |
54 |
49 |
43 |
36 |
28 |
21 |
15 |
| 61 |
58 |
54 |
49 |
43 |
36 |
28 |
21 |
| 63 |
61 |
58 |
54 |
49 |
43 |
36 |
28 | |
- 位移完成后,最后一步就是用“屏蔽模版”将需要的数据分离出来。“屏蔽模版”根据斜线的长度不同而变化。
-
- Mask_Length = (2 ^ diag_length) - 1;
-
- 按照这个公式,当斜线的长度为7时,屏蔽模版等于127(二进制:1111111b)。如果斜线的长度为1时屏蔽模版也为1。在程序中你可以用这个公式,但是使用查询表会更快一些。
-
- 索引 diag_H8A1_attacks[64][256] 数组。
- 为了对齐H8->A1方向的斜线,我们要把棋盘向右旋转45度。(再来一杯可乐?)
-
- int r45R_map[64] = {
- 0, 1, 3, 6, 10, 15, 21, 28,
- 2, 4, 7, 11, 16, 22, 29, 36,
- 5, 8, 12, 17, 23, 30, 37, 43,
- 9, 13, 18, 24, 31, 38, 44, 49,
- 14, 19, 25, 32, 39, 45, 50, 54,
- 20, 26, 33, 40, 46, 51, 55, 58,
- 27, 34, 41, 47, 52, 56, 59, 61,
- 35, 42, 48, 53, 57, 60, 62, 63
- };
- BitBoard Rotated45R = 0;
- for (棋盘上的每一格)(0-63) {
- if square is not empty
- Rotated45R |= mask[r45R_map[square]];
- }
|
需要右移的位数 |
| 0 |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
| 1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
| 3 |
6 |
10 |
15 |
21 |
28 |
36 |
43 |
| 6 |
10 |
15 |
21 |
28 |
36 |
43 |
49 |
| 10 |
15 |
21 |
28 |
36 |
43 |
49 |
54 |
| 15 |
21 |
28 |
36 |
43 |
49 |
54 |
58 |
| 21 |
28 |
36 |
43 |
49 |
54 |
58 |
61 |
| 28 |
36 |
43 |
49 |
54 |
58 |
61 |
63 | |
- 最后,像对第一根斜线所做的那样,分离出所需数据。
- 对这两个位棋盘做“逻辑或”,便得到记录受象攻击的格子的位棋盘。
-
- bishop_attack = diag_A8H1_attacks | diag_H8A1_attacks;
-
- 最后,要得到受皇后攻击的格子的位棋盘,只要把受车攻击的格子“或”上受象攻击的格子:
-
- queen_attack = rook_attack | bishop_attack;
-
- 【一位网友来信说他剖析过 Galahad 的源程序,程序中并未发现“旋转的位棋盘”的算法,而采用一种“位行”(BitRank)和“位列”(BitFile)的结构。正摆的位棋盘实际上就是把8个位行连在一起形成的,而旋转90度的位棋盘则是由8个位列连在一起的,至于旋转45度和315度的位棋盘,实际上也只需要用两套15个的“位斜线”就可以了。比起位行和位列操作,通过位移运算从位棋盘中析取某行或某列,就显得多此一举了,因此它的效远远没有位行和位列高。而旋转的位棋盘这种炫技,它的作用仅仅是误导一下象棋引擎设计师而已。】
-
- 出处:不详
- 译者:Allen Liu (ditch_u@{域名已经过期},)
- 类型:不详
- 编辑:黄晨 (webmaster@{域名已经过期})
 关闭窗口  打印文档 |














 账号登录
账号登录