棋盘的表示-游戏开发 - 常州市武进区嘉泽中心小学

栏目列表

您现在的位置是：首页>>教师>>计算机技术>>程序设计>>游戏开发>>文章内容

棋盘的表示

发布时间：2008-11-20 点击：来源：本站原创录入者：David Eppstein

　　要让机器下棋，程序首先必须对两个对象进行存储和操作，它们是局面和着法。这两个对象的表示使得程序可以进行下列操作：

　　(1) 执行一个着法(不仅仅是用户所指出的着法，而是在搜索过程中要用到的)；

　　(2) 撤消一个着法(作用同上)；

　　(3) 向用户显示棋盘；

　　(4) 产生所有可能的着法；

　　(5) 对棋盘的局面作出评估。

　　除了显示棋盘以外，所有的操作都应该尽可能地迅速，因为它们会在搜索的循环内被调用。(而显示棋盘的操作毕竟不是经常要做的。【译注：在UCI协议(国际象棋通用引擎协议)中，引擎从不显示棋盘，因此这个操作事实上是多余的。】)

　　着法的内部表示应该是非常简洁的(因为我们不需要花太多的时间来生成一系列着法)而且能快速解读，但是非常重要的是，它应该能代表所有的着法！在国际象棋中，机器内典型的着法表示，就是记录移动棋子的起点格子和终点格子，例如王前兵进两格就表示为“e2e4”(e2代表这个兵起点位置而e4代表终点位置)。不管是否吃子，被吃的棋子都不必记录，因为它可以由终点格子来判断。在机器中位置能表示为6位的数值，所以一个着法可以用2个字节表示。尽管很多程序都是这样表示的，但是这种表示方法不足以表示所有的着法！王车易位时，有两个子要移动，此时我们把它当作特殊情况来考虑，只记录王的移动。问题在于，当兵从第七行走到第八行时，可以升变为后、车、马或象，上述表示方法不能让我们指定升变为哪个棋子。因此在设计着法表示时需要非常仔细，要确认这种表示能够涵盖棋局中所有可能发生的特殊情况。

　　【一般而言，棋类的着法有两种形式，即添子式和移动式。五子棋、围棋、黑白棋等属于添子式，记录着法时只要记录棋子所下到的那个格子。其中五子棋最简单，下完的棋子不再会改变；黑白棋稍复杂些，下完的棋子可能会被后续着法所变换黑白，但每下一子棋盘上就多一子；围棋是最复杂的，由于存在提子的着法，所以局势是可逆的，打劫这样的着法需要很复杂的处理过程。

　　国际象棋和中国象棋都属于移动式，相比较而言中国象棋更简单，当一个棋子从起点移到终点时，只要简单地做一下终点的覆盖即可；而国际象棋由于三条特殊规则的存在而必须做特别处理，有时别的特殊位置的棋子要跟着移动(王车易位)，有时别的特殊位置的子要被吃掉(吃过路兵)，有时移动的棋子要被其他棋子所替代(升变)。】

　　棋盘的表示可能稍许复杂了些，但也不应该太庞大。它必须包括所有相关的信息，而不仅仅是表观上的，但无关的信息不包括在其中。例如在国际象棋里，我们必须知道棋子在棋盘上的位置(表观上的信息)，而且需要知道一些不可见的信息——现在是谁在走，每方是否还有易位权，哪个过路兵可以吃，从吃子或进兵到现在一共走了多少步。我们还需要知道以前发生过哪些重复的局面(因为三次重复局面即导致和棋)，而不需要知道以前所有的着法。

　　【在网络通讯中常常用一种称为FEN串的6段式代码来记录局面，在国际象棋中它的6段代码依次为：棋盘、走子方、王车易位权、吃过路兵的目标格、可逆着法数以及总回合数，基本上涵盖了国际象棋某个局面的所有信息。但是FEN字符串无法记录重复局面，因此UCI协议中规定，局面由棋局的最后一个不可逆局面(发生吃子、进兵或升变的局面)和它的后续着法共同表示，这样就涵盖了重复局面的信息。】

举例说明国际象棋中的诸多棋盘表示方法

　　国际象棋中有很多表示棋盘的方法，以下这些是程序中可能用到的：

　　一、棋盘格子的8x8数组

　　每个格子的值代表格子中的棋子(例如：enum { empty, wK, wN, wB, wR, wQ, wP, bK, bN, bR, bQ, bP })。它的优点在于：(1) 简单；(2) 容易计算子力价值：

for (i = 0; i < 8; i ++)

　for( j = 0; j < 8; j ++)

　　score += value[square[i, j]];

　　计算可能的着法有些麻烦但并不非常困难，可以找遍棋盘的每个格子，根据棋子的颜色和类型来做分枝：

for (i = 0; i < 8; i++) {

　for(j = 0; j < 8; j++) {

　　switch (board[i, j]) {

　　case wP:

　　　if (board[i + 1, j] = empty) {

　　　　生成到(i + 1, j)的着法;

　　　}

　　　if (i == 2 && board[i + 1, j] == empty && board[i + 2, j] empty) {

　　　　生成到(i + 2, j)的着法;

　　　}

　　　if (j > 0 && board[i + 1, j - 1]有黑子) {

　　　　生成吃(i + 1, j - 1)子的着法;

　　　}

　　　if (j < 7 && board[i + 1, j + 1]有黑子) {

　　　　生成吃(i + 1, j + 1)子的着法;

　　　}

　　　break;

　　　...

　　}

　　但是很多检测边界的判断(例如，兵在车一路就不能吃更外侧的子)，使得代码非常复杂，速度非常缓慢。

　　二、扩展数组

　　包括扩展边界的10x10数组，在棋子类型中应包括“boundary”这个值。这样就可以花很少的代价，来简化一些判断。【在下面提到的0x88方法问世以前，最普遍的做法却是用12x12的数组(即有双重的扩展边界)，这样连马的着法也不用担心跳出棋盘了。】

　　三、0x88

　　这个名称来自一个技巧——通过判断格子编码是否包含136这个数(在16进制中是0x88)来检测着法是否合理。下表就是格子的编码(用一个字节)，高4位表示行，低4位表示列。

120	121	122	123	124	125	126	127
96	97	98	99	100	101	102	103
80	81	82	83	84	85	86	87
64	65	66	67	68	69	70	71
48	49	50	51	52	53	54	55
32	33	34	35	36	37	38	39
16	17	18	19	20	21	22	23
0	1	2	3	4	5	6	7

　

　　这样，格子i的左边一格是i - 1，右边是i + 1，上边是i + 16，下边是i - 16，等等。棋盘被表示为128个格子的数组(其中64格代表棋盘上存在的格子)，这种表示的优势在于：(1) 数组仅用1个指标，这样写的程序要比用2个指标快；(2) 可以快速简单地判断某个格子i是否在棋盘上——当且仅当(i & 0x88) == 0时i在棋盘上。(因为列超出范围时i & 0x08不为零，而行超出范围时i & 0x80不为零。)这是一个非常有效而且常用的技巧。

　

　　四、位棋盘

　　我必须在这里多花些笔墨，因为这个技术还不被人所熟悉，但是我认为它可能会很好用的。以前用一个格子数组，每个元素含有一个棋子，现在取而代之的是一个棋子数组，每个元素代表棋盘上哪几个格子有这个棋子，按位压缩表示。由于棋盘上有64个格子，所以棋盘可以压缩成一个64位的字(即两个32位的字)。这种表示最大的优势在于，可以通过布尔操作(位操作)来加快局面评估和着法生成操作的速度。试想一下，如此烦琐的事情可以用压缩的字运算来解决，例如下面的局面：

　

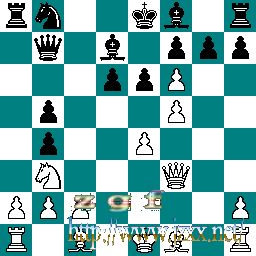
　　白方的兵(这个64位数字记作wP)应该由这些位构成：

　

0 0 0 0 0 0 0 0

0 0 0 0 0 1 0 0

0 0 0 0 1 0 0 0

0 0 0 0 0 0 0 0

1 1 1 0 0 0 0 1

0 0 0 0 0 0 0 0

　

　　而被黑方占据的格子可以用下面的公式来计算：

　

bOcc = bP | bN | bB | bR | bQ | bK

　

　　(这里bP等等代表黑方不同兵种的棋子)，类似地可以计算白方占据的格子，还可以把这两个格子作“或”运算得到所有被占的格子。这些白兵前进一格可能到达的格子，可以用下面的公式计算：

　

single_pawn_moves = (wP << 8) & ~occupied

　

　　现在仔细看一下过程，先将wP左移8位，来产生每个兵前面的格子：

　

0 0 0 0 0 0 0 0

0 0 0 0 0 1 0 0

0 0 0 0 1 0 0 0

0 0 0 0 0 0 0 0

1 1 1 0 0 0 0 1

0 0 0 0 0 0 0 0

　

　　然后求被占格子的“非”运算得到空的格子：

　

0 0 1 1 0 0 1 0

1 0 1 0 1 0 0 0

1 1 1 0 0 0 1 1

1 0 1 1 1 0 1 1

1 0 1 1 0 1 1 1

1 0 1 1 1 0 1 1

0 0 0 1 1 1 1 0

0 1 0 1 0 0 1 0

　

　　对以上两个位棋盘按位作“与”运算，就得到这些兵前面的没有被占的格子了：

　

0 0 0 0 0 0 0 0

0 0 0 0 1 0 0 0

0 0 0 0 0 0 0 0

1 0 1 0 0 0 0 1

0 0 0 0 0 0 0 0

　

　　参照兵走一格的方法，可以找到兵走两格的着法，即再左移8位，“与”上没有子的格子，再“与”上一个只有第四行都占满的常数棋盘(这是兵走两格能到达的唯一一行)：

　

0 0 0 0 0 0 0 0

1 1 1 1 1 1 1 1

0 0 0 0 0 0 0 0

　

　　值得注意的是，这个常数棋盘是在编译的时候生成的，而不需要在每次着法生成的时候再计算出来。兵吃子的情况也类似，先左移7位或9位，再“与”上一个常数棋盘以过滤左边线或右边线的格子【对于左移7位产生吃右边子时，需要考虑子在右边线的情况，此时左移7位是同一行的左边线，因此需要排除这个格子，即“与”上一个常数棋盘，代表除左边线以外的所有格子】，最后“与”上bOcc【前面提到过这个棋盘，代表黑子所占的格子】。

　　位棋盘这个技术不能简化代码，但是它能一次就产生兵的所有着法，而不是一次只产生一个着法。此外，这个过程中有些表达式需要多次反复使用(例如bOcc)，但只要计算一次就可以了。因此，位棋盘最终变得非常高效，在棋子数比国际象棋少的棋类中，我想位棋盘的效果会更好。

　　有个复杂的问题产生了：计算位棋盘中有多少非零位，或者找到【最低或最高的】一个非零位(例如把兵可以到达的位棋盘转化为一系列着法)，这些操作往往非常重要。计算位数的操作可以一次计算一个字节，做一个长度为256的数组，每个元素代表它的指标所含有多少个非零位，然后通过查表来完成。在找到一个非零位的计算中有个技巧：x ^ (x - 1)(“^”代表异或)，会得到一个二进制为...000111...的数，x ^ (x - 1)的第一位就是x的最后一位非零位。如果要求得这个数字【x ^ (x - 1)，即型如...000111...的数】的第一位，就把它对某个特定的数M取余数(不同的...000111...这样的数对M取余数必须不同)，然后去查表。例如，以下的代码可以找到一个字节的最后一个非零位：

int T = { -1, 0, 7, 1, 3, -1, 6, 2, 5, 4, -1, -1 };

int last_bit(unsigned char b) {

　return T[(b^(b-1)) % 11];

}

　

　　【把原作者提到的这个技巧扩展到16位或32位的情况，不妨可以试探一下(只要找得到合适的除数即可)。但是原作者没有充分考虑计算机的运算特点，因此译者认为这不是一个合理的设计。由于“电脑一做除法就成了傻瓜”，所以代码中取余数的过程严重影响了效率，为此译者收集了一些使用炫技的程序，可以迅速完成求位数和查找位的操作。

　　(1) 求一个32位数中有几位非零位的运算——Count32操作：

int Count32(unsigned long Arg) {

　Arg = ((Arg >> 1) & 0x55555555) + (Arg & 0x55555555);

　Arg = ((Arg >> 2) & 0x33333333) + (Arg & 0x33333333);

　Arg = ((Arg >> 4) & 0x0f0f0f0f) + (Arg & 0x0f0f0f0f);

　Arg = ((Arg >> 8) & 0x00ff00ff) + (Arg & 0x00ff00ff);

　return (Arg >> 16) + (Arg & 0x0000ffff);

}

　

　　(2) 求最低位非零位是第几位的运算——Lsb32操作(LSB = Least Significant Bit)：

int Lsb32(unsigned long Arg) {

　int RetVal = 31;

　if (Arg & 0x0000ffff) { RetVal -= 16; Arg &= 0x0000ffff; }

　if (Arg & 0x00ff00ff) { RetVal -= 8; Arg &= 0x00ff00ff; }

　if (Arg & 0x0f0f0f0f) { RetVal -= 4; Arg &= 0x0f0f0f0f; }

　if (Arg & 0x33333333) { RetVal -= 2; Arg &= 0x33333333; }

　if (Arg & 0x55555555) RetVal -=1;

　return RetVal;

}

　

　　(3) 求最高位非零位是第几位的运算——Msb32操作(MSB = Most Significant Bit)：

int Msb32(unsigned long Arg) {

　int RetVal = 0;

　if (Arg & 0xffff0000) { RetVal += 16; Arg &= 0xffff0000; }

　if (Arg & 0xff00ff00) { RetVal += 8; Arg &= 0xff00ff00; }

　if (Arg & 0xf0f0f0f0) { RetVal += 4; Arg &= 0xf0f0f0f0; }

　if (Arg & 0xcccccccc) { RetVal += 2; Arg &= 0xcccccccc; }

　if (Arg & 0xaaaaaaaa) RetVal += 1;

　return RetVal;

}

　

　　对64位数字进行操作，把它分解成两个32位字，分别对两个字调用上面的函数就可以了。如果程序能运行在64位的处理器上，只要对上面三个函数略加改动就可以了。】

　

如何撤消着法？

　

　　还记得吗？我们说过在棋盘表示方法中需要涉及撤消着法的操作。现在有两种解决方案：(1) 用一个堆栈来保存棋盘，执行一个着法前先将棋盘压入堆栈，撤消着法就从堆栈弹出棋盘，恐怕这太慢了…… (2) 用一个堆栈来保存着法，执行一个着法前先将该着法及其相关信息压入堆栈，撤消着法就根据该着法还原棋盘及其相关信息。例如，在国际象棋中只要保存被吃的棋子(如果吃子的话)，以及王车易位和吃过路兵的权利等信息。

　

重复检测

　

　　某些棋类在发生重复局面时要用到特殊的规则，如围棋和国际象棋(在国际象棋中，第三次出现重复局面时，制造重复局面的一方就有权宣布和棋)。那么如何知道是否出现重复局面呢？答案很简单：用散列函数把局面转换成一个相当大的数(我们以后要谈到这个问题，因为这个技术还可以加快搜索速度)，然后保存一系列前面出现过的局面的散列值，从这些值里面找就是了。一个典型的散列函数，先随机产生一张64x13的表，如果棋子y在位置x上，就把表中[x, y]这个数加到散列值上(忽略溢出)[即Zobrist值]。值得注意的是，当棋子y从位置x走到位置z时，可以快速地更新散列值：减去[x, y]并加上[z, y]即可。

　

　　原文：

　　译者：黄晨 (webmaster@{域名已经过期})

　　类型：全译加译注

附件：

关闭窗口

打印文档

账号登录




保持登录	忘记密码？
账号与武进教师培训平台同步